sinx的倒数是什么?
sinx的倒数是1/sinx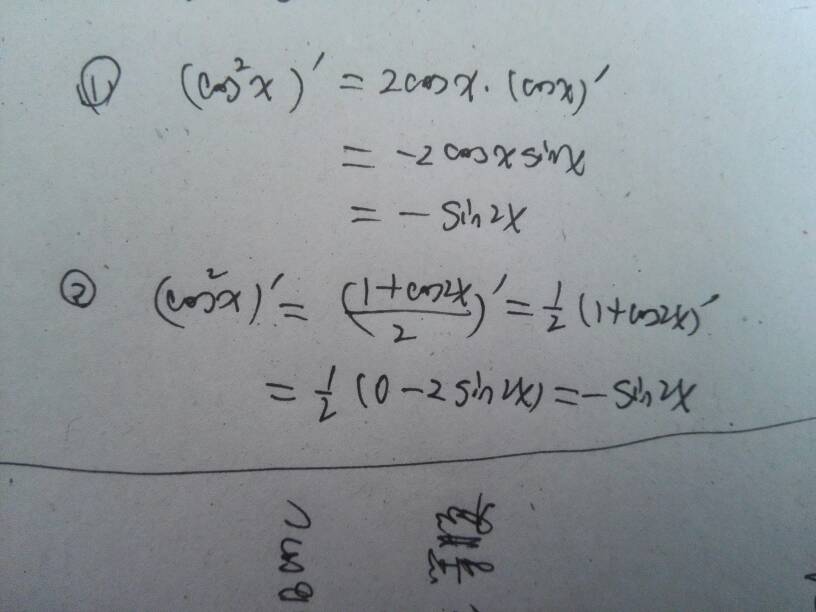
对于任意一个实数x都对应着唯一的角(弧度制中等于这个实数),而这个角又对应着唯一确定的正弦值sinx,这样,对于任意一个实数x都有唯一确定的值sinx与它对应,按照这个对应法则所建立的函数,表示为y=sinx,叫做正弦函数。
sinx是正弦函数,而cosx是余弦函数,两者导数不同,sinx的导数是cosx,而cosx的导数是 -sinx,这是因为两个函数的不同的单调区间造成的。
单位圆定义
图像中给出了用弧度度量的某个公共角。逆时针方向的度量是正角而顺时针的度量是负角。设一个过原点的线,同x轴正半部分得到一个角θ,并与单位圆相交。这个交点的y坐标等于 sinθ。在这个图形中的三角形确保了这个公式;半径等于斜边并有长度 1,所以有了 sinθ=y/1。
单位圆可以被认为是通过改变邻边和对边的长度并保持斜边等于 1 查看无限数目的三角形的一种方式。即sinθ=AB,与y轴正方向一样时正,否则为负,对于大于 2π 或小于 0 的角度,简单的继续绕单位圆旋转。在这种方式下,正弦变成了周期为 2π的周期函数。
sinx的倒数是什么?
sinx的导数是cosx(其中x为变量),sinX是正弦函数,而cosX是余弦函数,两者导数不同,sinX的导数是cosX,而cosX的导数是-sinX,这是因为两个函数的不同的升降区间造成的。
推导过程:
(sinx)'=lim/(△x),其中△x→0,
将sin(x+△x)-sinx展开,
sinxcos△x+cosxsin△x-sinx,由于△x→0,故cos△x→1,
从而sinxcos△x+cosxsin△x-sinx→cosxsin△x,
于是(sinx)’=lim(cosxsin△x)/△x,
△x→0时,lim(sin△x)/△x=1,
所以(sinx)’=cosx。
三角函数导数公式:
(sinx)'=cosx
(cosx)'=-sinx
(tanx)'=sec²x=1+tan²x
(cotx)'=-csc²x
(secx)'=tanx·secx
(tanx)'=(sinx/cosx)'=/cos²x=sec²x。
sin的倒数是什么?
正弦函数的倒数是余割。sinx=1/sinx=cscx。
余割为一个角的顶点和该角终边上另一个任意点之间的距离除以该任意点的非零纵坐标所得之商,这个角的顶点与平面直角坐标系的原点重合,而其始边则与正X轴重合。
在直角三角形中,斜边与某个锐角的对边的比值叫做该锐角的余割.记作cscx。
余割与正弦的比值表达式互为倒数。
余割函数为奇函数,且为周期函数。
图像中给出了用弧度度量的某个公共角。逆时针方向的度量是正角而顺时针的度量是负角。设一个过原点的线,同x轴正半部分得到一个角θ,并与单位圆相交。这个交点的y坐标等于sinθ。
在这个图形中的三角形确保了这个公式;半径等于斜边并有长度1,所以有了cscθ=1/y。单位圆可以被认为是通过改变邻边和对边的长度并保持斜边等于1查看无限数目的三角形的一种方式。
SINx的倒数是什么
SINx的倒数是1/sinx,其中x不等于k*pi pi是圆周率,k是任意整数
sinx的导数是cosx
sinx的反函数是arcsinx
sinx倒数是多少?
是导数,不是倒数,sinx的导数是cosx(其中x为变量),sinX是正弦函数,而cosX是余弦函数,两者导数不同,sinX的导数是cosX,而cosX的导数是-sinX,这是因为两个函数的不同的升降区间造成的。
推导过程:
(sinx)'=lim/(△x),其中△x→0,
将sin(x+△x)-sinx展开,
sinxcos△x+cosxsin△x-sinx,由于△x→0,故cos△x→1
从而sinxcos△x+cosxsin△x-sinx→cosxsin△x
于是(sinx)’=lim(cosxsin△x)/△x
△x→0时,lim(sin△x)/△x=1
所以(sinx)’=cosx
函数可导的条件:
如果一个函数的定义域为全体实数,即函数在其上都有定义,函数在定义域中一点可导需要一定的条件:函数在该点的左右导数存在且相等,不能证明这点导数存在,只有左右导数存在且相等,并且在该点连续,才能证明该点可导。
可导的函数一定连续;连续的函数不一定可导,不连续的函数一定不可导。