一、正方形的物体有哪些?
正方形的物体:积木、围棋棋墩、方糖、墨水盒、石膏正方体、啤酒箱、魔方、色子等等还有很多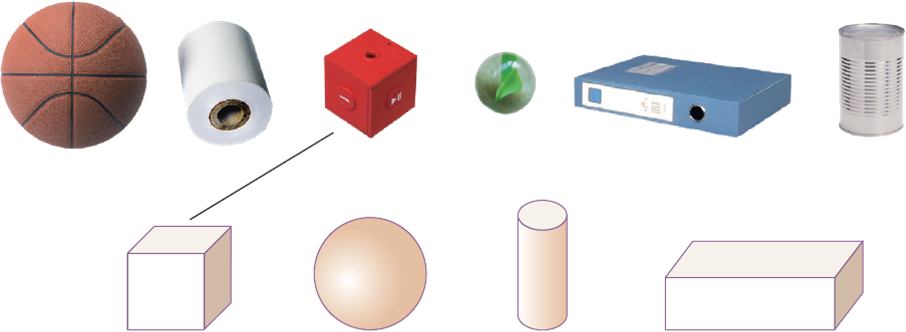
正方体特点
(1)正方体又叫正六面体。
(2)正方体有6个面、8个顶点、12条棱。
(3)正方体的六个面都是大小相同的正方形。
(4)正方体的侧棱都和底面垂直,所以正方体也属于直棱柱。
(5)正方体是底面是正方形的直四棱柱,所以正方体也属于正四棱柱。
(6)正方体是棱长都相等的长方体,所以正方体也是特殊的长方体。
(7)正方体的对称性质非常好,其对称中心在正方体体对角线的交点位置,也在每条体对角线的中点位置。
数正方体棱数、面数、顶点数的方法技巧
1、棱数
正方体的棱可以分为上、中、下三层。
最上层和最下层的底面都是一个正方形,各有四条棱;中间有四条侧棱。所以,一共有4+4+4=12条棱。
2、面数
面也可以分为上、中、下三层。
上、下层分别为上下底面,中间有4个侧面。所以一共有1+4+1=6个面。
3、顶点数
正方体的顶点可以分为上、下两层。
因为上、下层的底面都是正方形,每个正方形都有四个顶点。所以,一共有4+4=8个顶点。
一线教育名师,其它相关“正方体棱长总和公式和正方体的特点”的中学数学问题,可以点击下方卡片提问以便及时获得一对一的针对性帮助。
二、正方形的东西有哪些?
正方体的常见物品有:魔方、骰子、豆腐 、木箱、围棋棋墩等。六个完全相同的正方形围成的立体图形叫正六面体,也称立方体、正方体。正六面体是一种侧面和底面均为正方形的直平行六面体,即棱长都相等的六面体。正六面体是特殊的长方体。正六面体的动态定义是:由一个正方形向垂直于正方形所在面的方向平移该正方形的边长而得到的立体图形。
正方形具有以下性质:
1、两组对边分别平行;四条边都相等;邻边互相垂直。
2、四个角都是90°,内角和为360°。
3、对角线互相垂直;对角线相等且互相平分;每条对角线平分一组对角。
4、既是中心对称图形,又是轴对称图形并有四条对称轴。
5、正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的夹角是45°;正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
6、正方形具有平行四边形、菱形、矩形的一切性质与特性。
7、在正方形里面画一个最大的圆(正方形的内切圆),该圆的面积约是正方形面积的78.5%[4分之π];完全覆盖正方形的最小的圆(正方形的外接圆)面积大约是正方形面积的157%[2分之π]。
8、正方形是特殊的矩形,正方形是特殊的菱形。
三、正方体有哪些物品?
正方体物品:
1、积木。方形积木是立方的木头或塑料固体玩具,积木表面上装饰着字母或图画,可以进行不同的排列或进行建筑活动。
2、魔方。魔方是由富有弹性的硬塑料制成的正方体,核心是一个轴,并由一个个小正方体组成。
3、色子。色子是一种游戏用具,是用骨头、木头等制成的立体小方块,六面分刻一二三四五六点,一般用于麻将、棋牌类等汉族民间博艺活动。
几何性质
立方体是唯一能够独立密铺三维欧几里得空间的柏拉图正多面体,因此立方体堆砌也是四维唯一的正堆砌(三维空间中的堆砌拓扑上等价于四维多胞体)。它又是柏拉图立体中唯一一个有偶数边面——正方形面的,因此,它是柏拉图立体中独一无二的环带多面体(它所有相对的面关于立方体中心中心对称)。
将立方体沿对角线切开,能得到6个全等的正4棱柱(但它不是半正的,底面棱长与侧棱长之比为2:√3)将其正方形面贴到原来的立方体上,能得到菱形十二面体(Rhombic Dodecahedron)(两两共面三角形合成一个菱形)。
四、家里哪些东西是正方体?
日常生活中有很多东西都是正方体的,比如常见的方形积木、方形纸盒、粉笔盒、豆腐、木箱、方形积木、魔方、骰子、围棋棋墩、部分纸巾盒、石膏正方体、啤酒箱等。
正方体一般指正六面体。用六个完全相同的正方形围成的立体图形叫正六面体,也称立方体、正方体。
正六面体是一种侧面和底面均为正方形的直平行六面体,即棱长都相等的六面体。由一个正方形向垂直于正方形所在面的方向平移该正方形的边长而得到的立体图形
正六面体是特殊的长方体。
扩展资料:
正方体体积计算公式: V = S×S×S = 边长×边长×边长
正方体表面积计算公式: = S×S×6 = 边长×边长×6个面
五、正方体的物品有哪些?
正方体的常见物品:积木、豆腐 、木箱、围棋棋墩、正方体石块、方糖、墨水盒、石膏正方体、啤酒箱、魔方、色子等等。
正六面体是一种侧面和底面均为正方形的直平行六面体,即棱长都相等的六面体。正六面体是特殊的长方体。正六面体有6个面,每个面面积相等,形状完全相同。
扩展资料
计算公式:
1、表面积
因为正六面体6个面全部相等,且均为正方形,所以正六面体的表面积S=6a² ,其中,a为正六面体的棱长,S为正六面体的表面积。
2、体积
正方体属于棱柱的一种,棱柱的体积公式同样适用,即体积=底面积×高。由于正六面体6个面全部相等,且均为正方形,所以,正六面体的体积=棱长×棱长×棱长。
设一个正方体的棱长为a,则它的体积:V=a×a×a=a³。