一、抛物线的焦点是什么?
抛物线的焦点是定点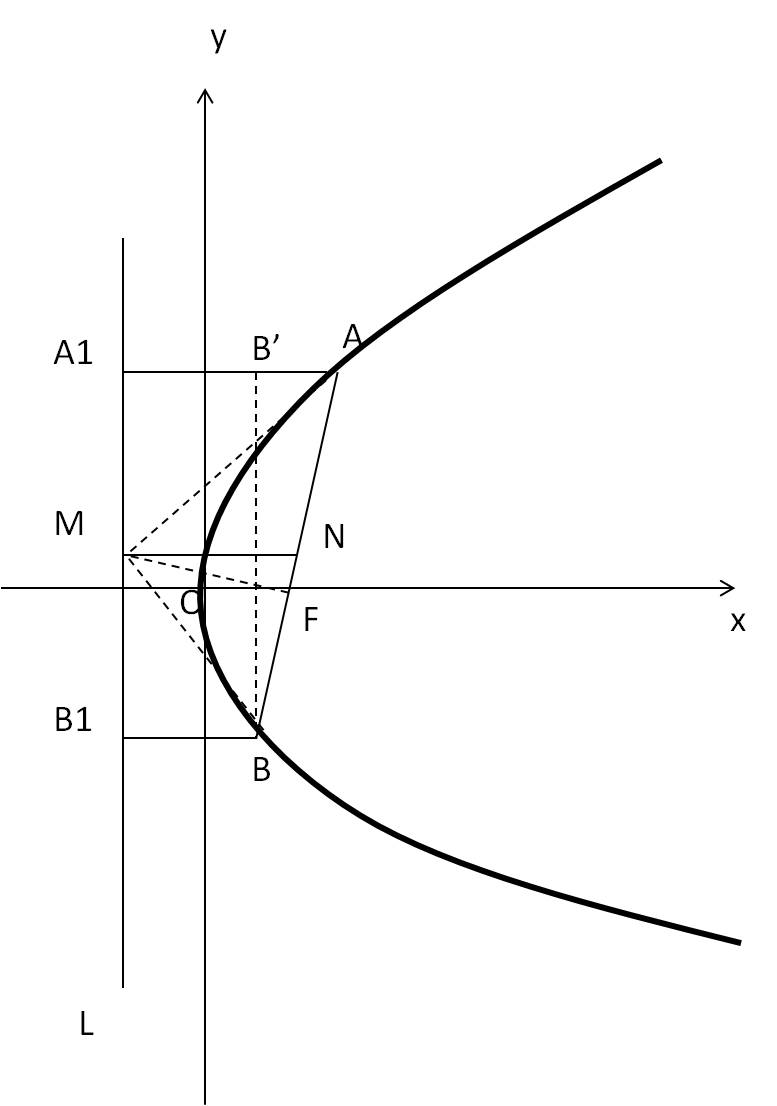
平面内,到定点与定直线的距离相等的点的轨迹叫做抛物线。其中定点叫抛物线的焦点,定直线叫抛物线的准线。
抛物线是指平面内到一个定点F(焦点)和一条定直线l(准线)距离相等的点的轨迹。它有许多表示方法。
发展历程
Apollonius所著的八册《圆锥曲线》(Conics)集其大成,可以说是古希腊解析几何学一个登峰造极的精擘之作。今日大家熟知的ellipse(椭圆)、parabola(抛物线)、hyperbola(双曲线)这些名词,都是Apollonius所发明的。
当时对于这种既简朴又完美的曲线的研究,乃是纯粹从几何学的观点,研讨和圆密切相关的这种曲线;它们的几何乃是圆的几何的自然推广,在当年这是一种纯理念的探索,并不寄望也无从预期它们会真的在大自然的基本结构中扮演着重要的角色。
二、什么叫做抛物线的焦点???
平面内,到定点与定直线的距离相等的点的轨迹叫做抛物线。其中定点叫抛物线的焦点。
焦点是指构建曲线的特殊点。
例如,一个或两个焦点可用于定义圆锥截面,其四种类型是圆形,椭圆形,抛物线和双曲线。 此外,使用两个焦点来定义卡西尼椭圆和笛卡尔椭圆,并且使用两个以上焦点来定义n-椭圆。
扩展资料
抛物线是椭圆的极限情况,其中的一个焦点是无限远的点。
抛物线上任意一点与焦点之间的所连线段的长度,叫做焦半径;过抛物线焦点的直线被抛物线截得的线段叫做焦点弦。
根据两个焦点定义圆锥:
椭圆可以定义为到两个给定焦点的距离之和为常数的点的轨迹。
圆是椭圆的特殊情况,其中两个焦点彼此重合。
因此,可以更简单地将圆定义为每个距离单个给定焦点的固定距离的点的轨迹。 也可以将圆定义为阿波罗尼奥斯圆,就两个不同的焦点而言,作为具有与两个焦点的距离的固定比例的点集合。
参考资料百度百科-焦点
百度百科-抛物线